3S is the abbreviation for “Seiwa Scholars Society,” which consists of the past and current Inamori Research Grant recipients. The 3S has evolved since 1997 with the hope that the interactions among the various specialties of the 3S members can lead to the further development of the research of their own. In the series “Visiting 3S Researchers,” we interview researchers in 3S who are very active in a variety of fields. The 12th interview is with Dr. Sho Tanimoto (2019 Inamori Research Grant Recipient) from Nagoya University.

On a geometric figure determined by an equation involving multiple terms and variables, how many rational points are there?—One of the most famous problems in an academic discipline that considers such questions is Manin’s Conjecture. Dr. Sho Tanimoto of Nagoya University, a researcher of Manin’s Conjecture, has delivered significant achievements in this field. If you’re not a mathematician, however, you probably have no idea what “research on Manin’s Conjecture” is. What exactly is Manin’s Conjecture, what is the significance of studying this problem, and what does it mean to study mathematics? We took this opportunity to ask Dr. Tanimoto these questions.

──What is “Manin’s Conjecture” that you study, Dr. Tanimoto? Could you explain it in a way that even people unfamiliar with mathematics can understand?

Dr. Tanimoto (title omitted below)　Sure. Let me try (laugh). To give you a broad framework, there is one branch of mathematics called Diophantine geometry. I’ll come back to this later, but for now, Manin’s Conjecture can be said to be one of conjectures in Diophantine geometry and was proposed by Yuri Manin and his collaborators in the late 1980s.

Then, you might ask, “What is Diophantine geometry?”

First, I want you to imagine geometric shapes like circles or cones. Just as a circle can be expressed as \(x^2+y^2=r^2\), these shapes can be represented by equations involving variables like \(x, y\) and \(z\).

A cubic surface model represented by \(x^3+y^3+z^3+w^3=0\)

Geometric shapes determined by equations of multivariable polynomials like this are called algebraic varieties. For example, the equation \(x^3+y^3+z^3+w^3=0\) can be depicted as a cubic surface in three-dimensional space shown above. For more complex and higher-dimensional equations, while drawing them or creating their models may not be possible, each equation corresponds to an algebraic variety with geometric properties in its respective dimension.

Diophantine geometry is a field of study that focuses on rational points on algebraic varieties like this, that is, points with coordinates given as rational numbers. Now, what is Manin’s Conjecture? Roughly speaking, it posits that there is a certain regularity in the number of rational points on a type of algebraic variety called “Fano varieties*¹.” In other words, Manin’s Conjecture asserts that the count of rational points on any Fano variety can be expressed by a single formula reflecting the geometric properties of that variety.

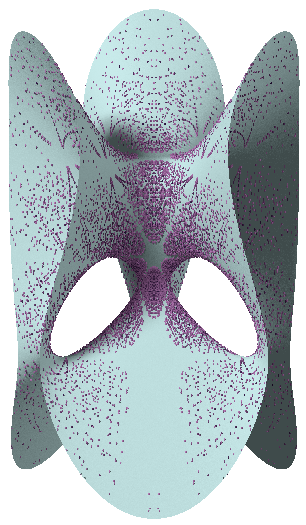
Rational points of bounded height outside the 27 lines on Clebsch’s cubic surface
©Drs. Ulrich Derenthal and Oliver Labs

Challenging Conjectures Gives Rise to New Mathematics

──I see. From what I gather, Manin’s Conjecture revolves around predictions concerning the count of rational points on geometric figures called algebraic varieties. But why do you study such a conjecture in the first place? Could you be kind enough to tell us about the mathematical significance of studying rational points on geometric figures or counting their numbers?

Tanimoto　When asked about the significance of studying Manin’s Conjecture, it’s never easy to give a straightforward answer. In fact, it’s not necessarily the case that there is immediate mathematical significance in counting the number of rational points. Or even if Manin’s Conjecture were proven, it wouldn’t necessarily have instant practical applications. That said, this doesn’t mean that such research is devoid of any meaning.

For instance, in Diophantine geometry, there is the well-known problem of “Fermat’s Last Theorem.” Jotted down by a 17th-century mathematician by the name of Fermat in the margin of a book along with the words, “I have a truly marvelous demonstration of this proposition that this margin is too narrow to contain.” This theorem is widely known for the fact that it took 350 years before it was proven.

This problem also concerns the count of rational points on a curve, and proving it didn’t have any specific mathematical significance or practical application. The fact is, however, as many mathematicians struggled to prove it over 350 years, it led to the birth of a great deal of new mathematics. In other words, it significantly contributed to making the world of mathematics more profound and rich.

The same goes with Manin’s Conjecture. It’s not that proving it leads to any practical application. Yet, to prove this conjecture, you need to use everything you know about algebra, geometry, and analysis, combining various branches of mathematics. In fact, Manin’s Conjecture is a highly interdisciplinary problem, with many mathematicians from multiple fields engaging with it. What this implies is that many mathematicians consider this conjecture important and that working on such problems has the potential to give rise to a large number of new mathematics.

Dr. Tanimoto explaining his complex research topic with care and enthusiasm

──Is it common to have such cases in mathematical research?

Tanimoto　Not necessarily, but in Diophantine geometry, one could argue that its value basically lies in the emergence of new mathematics as you attempt to solve the problems.

The new mathematics thus born in unexpected ways is actually of great use in society. For instance, modern encryption techniques utilize algebraic geometry and number theory, but researchers in those fields might not have initially imagined their work would be applied in such a manner. Mathematics is unpredictable in how and in what form it proves useful. This is where you find significance in pursuing mathematical research.

Research that Saved Manin’s Conjecture from a “Crisis”

──I think I have a good understanding of the background behind studying Diophantine geometry and Manin’s Conjecture now. Could you please share with me what aspects of Manin’s Conjecture you are personally researching?

Tanimoto　I have studied various aspects of Manin’s Conjecture, but if I cite one particularly significant aspect of my research, it is the study of “exceptional sets.”

Manin’s Conjecture posits a certain regularity in the number of rational points on Fano varieties, suggesting that a single formula can express it. Some rational points accumulate at sections that are exceptional in the whole region of a variety, such as the lines on a cubic surface. This being the case, such exceptional rational points, i.e., exceptional sets, need to be considered separately as they may distort the understanding of the overall structure of the variety. In the 1990s, counterexamples of a version of Manin’s Conjecture emerged, raising doubts about its validity. In response, my collaborators and I conducted a proof that geometrically defines and clarifies how to handle exceptional sets*². This proof shed light on the significance of the previously considered counterexamples and increased the credibility of Manin’s Conjecture. As a result, this research has garnered significant attention within the academic community.

──That’s wonderful! It was the research that saved Manin’s Conjecture from a crisis. My next question is, “What research topic are you focusing on these days?”

Tanimoto　Recently, I have been proposing “Geometric Manin’s Conjecture,” a curve version of Manin’s Conjecture, and I’m doing intensive research on it. While the original Manin’s Conjecture concerns counting rational points on varieties, this version counts curves on varieties. A crucial mathematical analogy exists here, and trying to understand Geometric Manin’s Conjecture, I believe, will lead to the elucidation of the properties of algebraic varieties.

I May Not See the Proof Within My Lifetime…

──In what stage is the proof of Manin’s Conjecture? Is it a case that it will be proven in the near future?

Tanimoto　Thirty years have passed since Manin’s Conjecture has been proposed. To be honest, there is no prospect of it being proven. Manin’s Conjecture encompasses predictions for all Fano varieties of every dimension, but we have yet to prove cases like cubic surfaces represented by equations like \(x^3+y^3+z^3+w^3=0\), which I introduced at the outset. Even proof for this would likely make headlines within the academic community. That’s how challenging the task of proving them is. It’s very possible that I won’t see the proof within my lifetime (laugh).

──Is that right? Do you not find it demotivating that you may not be able to prove it yourself?

Tanimoto　In a sense, the game is over when a conjecture is proven. If proven, some people will lose their jobs (laugh). Of course, it would be fantastic if we could prove it, but even without proof, the research on Manin’s Conjecture has already spawned a wealth of new mathematics. In this sense, doing research has tremendous value in itself, even if you cannot reach the proof. Or you could probably say that all mathematicians are doing what they’re doing simply because they find it fascinating. Whether or not you could prove it may not necessarily be the most important aspect of the endeavor.

Currently dedicated to mathematics, Dr. Tanimoto began playing the guitar in junior high school and formed an alternative rock band in high school.

The Joy of Mathematical Research is in the Discussions with Others

──What made you become a researcher of Manin’s Conjecture?

Tanimoto　As a high school student, I longed to be a theoretical physicist, and I wanted to study superstring theory and the like. I remember during one summer break, I got so excited because my physics teacher gave a lecture on special relativity theory.

When I enrolled in the Tokyo Institute of Technology to study mathematics and physics, I became aware of my interest in the mathematical formulation of physics, and I chose to enter the Department of Mathematics in my second year. When I got to decide which laboratory to join for my senior year, I joined the algebraic geometry laboratory, which is also closely connected with theoretical physics. Then, for my graduate education, I deliberately chose New York University (NYU), partly because I wanted to live in the U.S.

At the NYU graduate school commencement

In my second year at NYU graduate school, I had the fortune of having Dr. Yuri Tschinkel, a specialist in Manin’s Conjecture, as my mentor. When I became a second-year student and passed a qualifying examination, being ready to start research any time, Dr. Tschinkel gave me a problem on Manin’s Conjecture, saying he wanted me to solve it the day after (laugh). That, in fact, brought me to research of Manin’s Conjecture.

──I’m curious how mathematicians do their research. Could you tell us something about your style as a researcher?

Tanimoto　In my case, before working on a major problem, I start by drawing up strategies as to how I should go about solving it and segmenting the problem into small steps. Then, I try solving the steps one by one. In doing so, I try as many ideas as possible, do calculations, and start writing a proof as if I’m writing an academic paper. Doing so lets me see if something is not good or not right. I then try another set of ideas and repeat this process.

I cherish having discussions with others, sharing my ideas with other mathematicians to invite their comments, or listening to their ideas to give my feedback. As I engage in this process, new ideas are born, or new ways are opened, per se. The proof regarding the exceptional sets in Manin’s Conjecture, which I mentioned earlier, is a joint research effort with Dr. Brian Lehmann of Boston College. He is a very good friend of mine, and we often have discussions and co-author papers. In terms of our expertise, he leans more towards algebraic geometry, while my focus is more on arithmetic geometry. The combination of our knowledge has allowed us to produce a variety of research outcomes. When the pool of our knowledge falls short, we often reach out to other researchers to ask for help.

──I thought that when given a choice, mathematicians would prefer doing research alone.

Tanimoto　You have a point. I, too, have the impression that many researchers here in Japan do their studies independently. Partly because I spent my graduate and postdoctoral years in the U.S. and Denmark, most of my collaborators are from abroad. In the case of American mathematicians, in particular, most engage in research as they discuss with others. For me, that is the joy of being a researcher of mathematics.

That being the case, it was quite tough not being able to see Brian or other collaborators in person for discussions during the COVID-19 pandemic. Even so, we used to talk almost every week on Zoom. Now that it has recently become possible to travel abroad, we now enjoy frequent face-to-face discussions as we used to. It has made me realize anew the importance of meeting in person as things that took months to discuss on Zoom can now be resolved in just a week when we meet in person.

Frequently discussing with Dr. Lehmann on Zoom

Our Society Cannot Exist Without Mathematics

──Lastly, pardon me for asking this, but the general impression of mathematical research is that it doesn’t produce anything that is immediately useful. Still, I also feel that mathematical research will remain as important as ever. My question is, what do you think the meaning of doing mathematical research is? Please reiterate your thoughts on the matter.

Tanimoto　Not a few people wonder what the use of studying mathematics is. However, a wealth of new mathematical knowledge is frequently utilized behind technologies that play crucial roles in today’s society, such as information science, AI, and cryptography. Without research in mathematics, our society as we know it would not exist.

On the other hand, one characteristic of mathematics is that you can’t say how studying this field will be of use. In other words, the innovations brought about by mathematics are simply unpredictable. Even while you engage in research just because you find it “interesting” without any purpose, the results can change the world in unexpected ways. That’s mathematics and as a researcher, I find value and fascination in this aspect of mathematics. Going forward, I hope to take on new challenges proactively, keeping in mind these nuances of mathematics.

Also, when you study mathematics in high school, you might wonder if there still is something left to research in mathematics. The fact is, there is still so much to explore. If you’re considering pursuing a path in mathematics, why don’t you take the leap and knock on the door of the mathematics department?

──Thank you so much!

*1 One of the main classifications of algebraic varieties. Including conics and cubic surfaces, this type of algebraic variety is relatively easy to handle.

*2 Brian Lehmann, Sho Tanimoto. “On the geometry of thin exceptional sets in Manin’s conjecture.” Duke Mathematical Journal, 166(15) 2815-2869 15 October 2017.
https://doi.org/10.1215/00127094-2017-0011

This Book

The Martian by Andy Weir, Penguin Random House This book was adapted into a film of the same title, starring Matt Damon. Dr. Tanimoto read the English version. “This is a novel about an astronaut stranded on Mars doing everything he can to survive and return to the Earth. It’s interesting, and I really liked it. The author, Andy Weir, is very knowledgeable in science, and this book is also fascinating in terms of physics and engineering. I read most of his novels.”

By My Side

The first item that came to Dr. Tanimoto’s mind was his beloved MacBook, which is “an essential tool for writing papers.” “It might be surprising, but I don’t use paper and pen so much. I have a whiteboard at home, and I usually do calculations on it and then directly input the results into my MacBook to transcribe them into papers. Also, though not an item, my wife has been supporting me since high school. I have also always appreciated support from my son and daughter (10 and 3 years, respectively, as of the interview date). They are dear to me beyond all else!”

Sho Tanimoto
Associate Professor, Graduate School of Mathematics, Nagoya University. Received his B.S. from the Tokyo Institute of Technology and then his M.S. (Mathematics) and Ph.D. (Mathematics) from New York University. After Rice University in Texas and the University of Copenhagen in Denmark, he became an Associate Professor, Priority Organization for Innovation and Excellence (POIE), Kumamoto University, in 2018 before assuming the current position in 2021. His areas of research include algebraic geometry and arithmetic geometry. His co-authored paper on Manin’s Conjecture’s exceptional sets mentioned in the text, “On the geometry of thin exceptional sets in Manin’s Conjecture,” was published in an influential academic journal, Duke Mathematical Journal, in 2017.